Trójkąt Pascala

Trójkąt Pascala to trójkątna tablica liczbowa. Na górze trójkąta znajduje się liczba 1, a potem w każdym wierszu pod nią rosną liczby, zaczynając od jednej liczby na końcach, a następnie każda liczba wewnątrz to suma dwóch liczb nad nią w poprzednim wierszu. To powtarza się w każdym kolejnym wierszu, tworząc trójkąt z liczbami. Trójkąt Pascala ma wiele zastosowań w matematyce, w tym w kombinatoryce i teorii prawdopodobieństwa. Jest też bardzo użyteczny do rozwiązania różnych problemów związanych z kombinacjami i permutacjami.

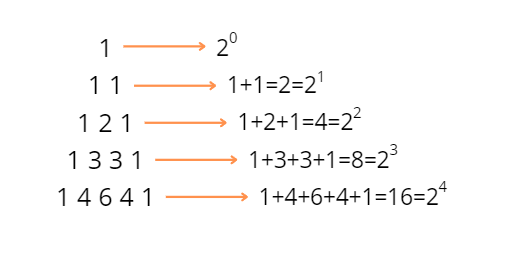
Własności trójkąta Pascala:

sumy liczb w kolejnych rzędach to kolejne potęgi liczby 2
w n-tej linii znajdują się kolejne współczynniki liczbowe rozwinięcia (a+b)^n
trójkąt Pascala można zapisać za pomocą dwumianu Newtona

Reprezentacja trójkąta Pascala za pomocą dwumianu Newtona:

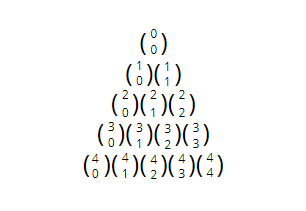
Przykładowa implementacja generowania Trójkąta Pascala:

#include <iostream>
using namespace std;
// Deklarujemy tablicę dwuwymiarową do przechowywania trójkąta Pascala
int p[10][10] = {0};
// Deklarujemy funkcja generująca trójkąt Pascala, jej argumentem będzie ilość tego
//ile wierszy trójkąta Pascala chcemy wypisać
void Pascal(int n)
{
    // Iterujemy się przez kolejne wiersze trójkąta
    for(int i = 0; i < n; i++) 
    {
        // Iterujemy się przez elementy w danym wierszu
        for(int j = 0; j <= i; j++) 
        {
            // Jeśli element jest na krańcach trójkąta przypisujemy mu wartość 1
            if(j == 0 || j == i) 
                p[i][j] = 1;
            else
                p[i][j] = p[i - 1][j] + p[i - 1][j - 1];
            //W przeciwnym razie obliczamy wartość elementu na podstawie
            //dwóch poprzednich
        }
        // Wyświetlamy dany wiersz trójkąta Pascala
        for(int j = 0; j <= i; j++) 
            cout << p[i][j] << "\t";
        cout << "\n";
    }
}
int main() 
{
    Pascal(9); // Wowołujemy funkcję trójkąta Pascala dla 9 wierszy
}

ZADANIE: napisz program, który wypisze kolejne współczynniki liczbowe dla wyrażenia (a+b)^n, gdzie n jest liczbą wczytaną z klawiatury