Systemy liczbowe

Czym są systemy liczbowe?

Jest to zbiór reguł co do sposobu zapisu liczb. Najbardziej powszechnym jest system dziesiętny, używany przez nas na co dzień, komputery jednak nie pracują w nim bezpośrednio. Odczytują polecenia za pomocą bitów, czyli systemu dwójkowego.

Podstawa	Cyfry, których możemy używać	System
x	o do x-1
2	0 do 1	Dwójkowy (binarny)
10	0 do 9	Dziesiętny
8	0 do 7	Ósemkowy
16	0 do 9, A do F	Szesnastkowy

Jeżeli mamy liczbę 249 zapisaną w systemie dziesiętnym, to w zapisie dwójkowym będzie ona składała się z 0 bądź 1, czyli będzie wyglądać tak: 11111001, a w systemie szesnastkowym może się składać z zarówno cyfr jak i liter, będzie więc wyglądać następująco: F9

Zamiana z systemu dziesiętnego na dowolny system:

Aby zamienić liczbę zapisaną w systemie dziesiętnym na jej reprezentację w dowolnym systemie (maksymalnie o podstawie 9, gdyż dla pozostałych będziemy używać również liter, więc będzie to wyglądało trochę inaczej) będziemy ją dzielić przez podstawę nowego systemu dopóki będzie większa od zera, a reszty zapiszemy w tablicy. Uzyskane reszty z dzielenia to kolejne cyfry liczby w podanym systemie. Pierwsza uzyskana reszta to ostatnia cyfra reprezentacji liczby, druga to przedostatnia itd.

Działanie algorytmu dla liczby 37 i podstawy 3:

kolejne cyfry reprezentacji liczby w systemie trójkowym	liczbę 37 chcemy zapisać w systemie o podstawie 3
37%3=1	37/3=12
12%3=0	12/3=4
4%3=1	4/3=1
1%3=1	1/3=0, osiągamy wartość zero, czyli kończymy obliczenia

#include<iostream>
using namespace std;
void to_binary(int x,int p)
//deklarujemy funkcję z dwiema zmiennymi: x i p
//x to liczba której reprezentacje będziemy obliczać dla systemu o podstawie p
{
    long long wynik=0,w=1;
//deklarujemy zmienną, w której będziemy przechowywać wynik, po kolei
//dodając do niej kolejne cyfry w jest zmienną, która będzie nam do tego niezbędna. 
//Pierwsza reszta z dzielenia którą otrzymamy będzie ostatnią cyfrą wyniku 
//moglibyśmy ją do niego po prostu dodać (gdyż początkowo jest on równy zero). 
//Druga reszta z dzielenia to przedostatnia cyfra wyniku, więc aby dodać ją 
//na odpowiednie miejsce mnożymy ją przez 10 i dodajemy do wyniku itd. 
//trzecią resztę z dzielenia pomnożymy przez 100, czwartą przez 100 - czyli 
//przez kolejne potęgi
    while(x>0)   //wykonujemy działania, dopóki x jest większy od 0
    {
        int m=x%p;  
        //zmiennej pomocniczej m przypisujemy resztę z dzielenia liczby x przez m
        x=x/p;  //dzielimy x przez p
        wynik=wynik+m*w;
        //do wyniku dodajemy wartość reszty z dzielenia pomnożoną przez kolejną potęge 10
        w=w*10; //mnożymy zmienną przez 10, aby otrzymać kolejną potęge 10
    }
    cout<<wynik;   //wypisujemy otrzymany wynik
}
int main()
{
    long long a;
    int p;
    cin>>a>>p;
    to_binary(a,p);  //wywołujemy funkcję dla odpowiednich argumentów
}

Zamiana z dowolnego systemu na system dziesiętny:

Zamieńmy teraz liczbę 11111001 z systemu binarnego na 10 (metoda ta działa dla zamiany dowolnego systemu liczbowego na dziesiętny, lekko inaczej jest jedynie przy systemie szesnastkowym)

Naszą liczbę numerujemy od końca, zaczynając od 0 -podobnie jak dla liczb w systemie dziesiętnym najmniejsze znaczenie mają cyfry jedności, a większe znaczenie cyfry setek czy tysięcy (jeżeli porównamy sobie liczbę 292 i 274, większa będzie ta, której cyfra dziesiątek będzie większa, nie ta, u której większa jest cyfra jedności, czyli większą liczbą jest 292), tak tutaj w podobny sposób nadajemy cyfrom wagę.

Teraz zaczynając od tyłu liczby każdą cyfrę mnożymy przez potęgę podstawy systemu, w którym znajduje się obecnie liczba (w naszym przypadku 2). Nasze potęgi to kolejne wartości, które przed chwilą nadaliśmy liczbom.

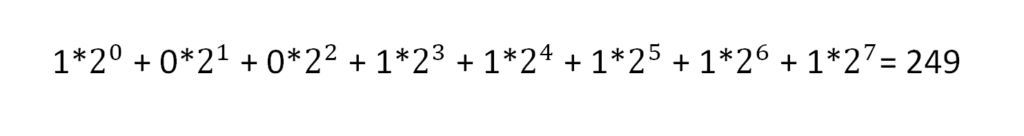
Wynikiem naszego równania będzie liczba w systemie dziesiętnym, czyli 249

# include <iostream>
using namespace std;
int main()
{
    int a=1, x;		
    //x będzie naszą zmienną pomocniczą zawierającą resztę z dzielenia
    //a potęgą podstawy przez którą będziemy mnożyć
    int liczba, podstawa;	
    //liczba to liczba którą zamieniamy, a podstawa to podstawa systemu
    //z którego chcemy zamienić liczbę
    int wynik=0;		//zmienna wynik zawierać będzie liczbę w systemie 10
    cin>>liczba>>podstawa;
    while(liczba>0)		//program wykonujemy dopóki nasza liczba będzie większa od zera
    {
        x=liczba%10;   //obliczamy resztę z dzielenia
        if(x>0)		
        //jeżeli nasza reszta jest większa od zera
        //(gdybyśmy mieli 0 nie ma sensu mnożyć bo wyjdzie zero)
        {
           wynik+=x*a;	//do wyniku dodajemy mnożemy tej reszty i potęgi jej odpowiadającej
        }
        a=a*podstawa;	//zwiększamy potęgę 
        liczba-=x;		//przechodzimy do kolejnej cyfry
        liczba=liczba/10;
    }
    cout<<wynik;
}

Zamiana z systemu dziesiętnego na szesnastkowy:

Zamiana na system szestnastkowy wygląda tak samo jak na dowolny system z systemu dziesiętnego. Dla reszt z dzielenia większych od 9 będziemy przypisywać następujące wartości:

Reszta z dzielenia przez 16	Przypisana jej litera	Kod ASCII
10	A	65
11	B	66
12	C	67
13	D	68
14	E	69
15	F	70

Będziemy to robić na podstawie ich kodów ASCII.

#include<iostream>
using namespace std;
void to_hexadecimal(int x)
//deklarujemy funkcje z jedną zmienną, którą będziemy zamieniać na system szesnastkowy
{
    string wynik="";
    //deklarujemy zmienną typu string na wynik, która początkowo może być pusta
    int k=0;
    //deklarujemy zmienną k, która będzie zliczała ilość cyfr reprezentacji liczby x, 
    //aby potem wyświetlić je w odpowiedniej kolejności, ponieważ do zmiennej 
    //wynik będą one wczytywane do końca
    while(x>0)
    //dopóki x jest większy od 0
    {
        k++;    //zwiększamy licznik znaków reprezentacji o jeden
        int m=x%16; //w zmiennej pomocniczej zapisujemy resztę z dzielenia x przez 16
        x=x/16; //dzielimy x przez 16
        if(m<10)
        {
            wynik.append(to_string(m));
        //jeżeli reszta z dzielenia jest mniejsza od 10 to do zmiennej dopisujemy wartość 
        //reszty aby to zrobić konwertujemy zmienną m na zmienną typu string za pomocą 
        //funkcji to_string()
        }
        else
        //w przeciwnym przypadku do zmiennej wynikowej będziemy dopisywać odpowiednie litery
        {
            wynik.append(1,m+55);
            //w funkcji append jak pierwszy argument musimy zapisać 1
            //dzięki temu do wyniku dopiszemy literę, a nie jej kod ASCII
            //Kod ASCII litery A to 65 czyli dla m=10, chcemy uzyskać 65, 
            //dla m=11 chcemy uzyskać kod ASCII liczby B czyli 66
            //Wzorem na to będzie zatem dodawanie do m 55.
        }
    }
    for(int i=k-1;i>=0;i--)
    //od końca wyświetlamy kolejne znaki zmiennej wynik za pomocą funkcji for
    {
        cout<<wynik[i];
    }
}
int main()
{
    int x;
    cin>>x;
    to_hexadecimal(x);
    //wywołujemy funkcję dla odpowiedniego argumentu
}

Zamiana z systemu szesnastkowego na dziesiętny:

Chcąc zamienić liczbę z systemu 16 na 10 robimy to dokładnie tak samo jak w przypadku pozostałych systemów z drobną różnicą – jeżeli napotkamy literkę zamieniamy ją na jej liczbowy odpowiednik:

A-10, B-11, C-12, D-13, E-14, F-15

Na przykładzie liczby F9 będzie to wyglądać w ten sposób:

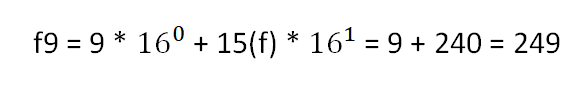
Tak wygląda przykładowa funkcja zamieniająca liczbę w systemie 16 na liczbę w systemie 10:

# include <iostream>
using namespace std;
int to_decimal(string x) 
{
    int wynik=0;	//tworzymy zmienną, która przechowa nasz wynik
    int potega=1;	//zmienna, która trzyma potęgę, do której podnosimy liczbę
    for(int i=x.length()-1;i>=0;i--)	//przechodzimy po naszej liczbie od tyłu
    {
        if (x[i]>='0' && x[i]<='9')		
        //jeżeli jest to liczba to wykonujemy to samo co
        //w przypadku zamiany z dowolnego innego systemu na 10
           wynik+=(x[i]-'0')*potega;
        else if (x[i] >= 'A' && x[i] <= 'F')		
        //jeżeli natomiast jest to litera to zamieniamy ją na liczbę 
        //poprzez odjęcie jej wartości w kodzie ascii (-‘A’) oraz dodajemy 10
        //ponieważ A w systemie 16 to 10, B to 11 itd.
            wynik+=(x[i]-'A' + 10)*potega;
        else if(x[i] >= 'a' && x[i] <= 'f')	//to samo zróbmy dla małych liter
            wynik+=(x[i]-'a' + 10)*potega;
        potega*=16;	//zwiększamy potęgę
    }
    return wynik;
}
int main()
{
    string liczba;
    cin>>liczba;
    cout<<to_decimal(liczba);  //wypisujemy wynik
}

Operacje bitowe:

Operacje bitowe to manipulacje na pojedynczych bitach w komputerze. Bit jest najmniejszą jednostką informacji i może przyjmować wartość 0 lub 1. Operacje bitowe pozwalają na wykonywanie różnych działań na tych bitach.

Oto kilka podstawowych operacji bitowych:

AND & (I): Operacja AND wykonuje logiczne “i” dla odpowiadających sobie bitów dwóch liczb. Wynikiem jest 1 tylko wtedy, gdy oba bity wejściowe są równe 1. W przeciwnym razie wynikiem jest 0.

OR | (Lub): Operacja OR wykonuje logiczne ‘lub” dla odpowiadających sobie bitów dwóch liczb. Wynikiem jest 1, jeśli jeden bądź dwa bity wejściowe są równe 1. Jeśli obydwa bity są równe 0 to wynikiem jest 0.

XOR ^ (Albo): Operacja XOR wykonuje logiczne “albo” dla odpowiadających sobie bitów dwóch liczb. Wynikiem jest 1, wtedy i tylko wtedy gdy dokładnie jeden bit jest równy 1. W przeciwnym przypadku wynikiem jest 0.

Przesunięcie bitowe:

Jest to dzielenie bądź mnożenie liczby zapisanej w systemie dwójkowym przez 2.

Zapisujemy je jako a>>b (przesunięcie w prawo) lub a<<b (przesunięcie w lewo).

W puste miejsca wpisujemy zawsze 0.

– w prawo (dzielenie)

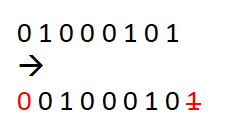
-w lewo (mnożenie)

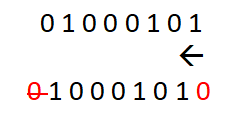
Trik na zamianę z systemu dwójkowego na czwórkowy:

Jeżeli podzielimy naszą liczbę zapisaną systemem dwójkowym na pary liczb możemy z łatwością odczytać ją zamienioną na system 4. Naszą liczbę dzielimy od tyłu i jeżeli brakuje nam cyfry, aby utworzyć parę wpisujemy tyle 0 ile potrzeba.

00	0
01	1
10	2
11	3

Zgodnie z tym 1001001011:

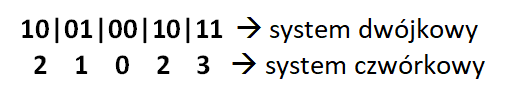
Trik na zamianę z systemu dwójkowego na ósemkowy:

Podobnie wygląda zamiana z systemu dwójkowego na ósemkowy. Tym razem jednak dzielimy naszą liczbę na trójki.

000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Liczba 1001001011 będzie więc wyglądać następująco:

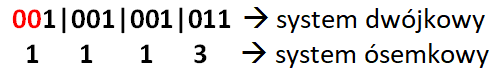
Dodawanie liczb binarnych:

W zapisie liczb binarnych mamy do dyspozycje dwie liczby, czyli możliwe podczas dodawania są 4 kombinacje:

1+0=0+1=1

0+0=0

1+1= 0 i 1 przenosimy dalej

Może nastąpić taki przypadek, że 1 przeniesiemy dalej a kolejnym dodawaniem będzie 1+1. Wtedy:

1+1+1=1 i 1 przenosimy dalej

Na przykładzie będzie to wyglądało następująco:

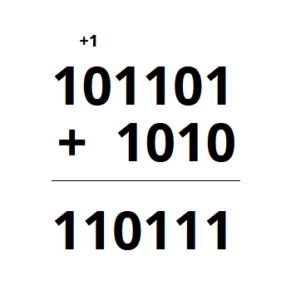
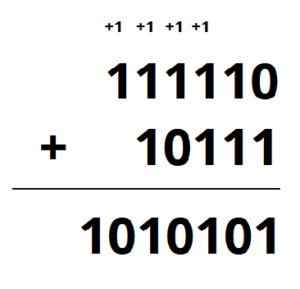
Zamiana ułamków na system binarny:

Przekształcenie ułamka dziesiętnego do postaci dwójkowej polega na odejmowaniu od konwertowanego ułamka kolejnych ujemnych potęg liczby 2.

2 do potęgi -1 to 1/2, 2 do -2 to 1/4 itd.

Na początku od ułamka odejmujemy 1/2:
– jeśli dana różnica byłaby ujemna, to po przecinku zapisujemy zero i nie zmieniamy wartości naszej liczby

– jeśli dana różnica byłaby dodatnia bądź równa zero, to po przecinku zapisujemy 1 i odejmujemy od naszej liczby 1/2

Tą czynność powtarzamy dla kolejnych potęg 1/4, 1/8, 1/16 aż do momentu gdy nasza początkowa liczba będzie równa zero.

Działanie algorytmu dla liczby 0,625:

Liczba a	Potęga liczby 2	Działanie	Wynik w systemie binarnym
0,625	2^-1=0,5	0,5<=0,625, więc: a=0,625-0,5=0,125	dopisujemy 1 po przecinku: 0,1
0,125	2^-2=0,25	0,25>0,125, więc a pozostaje tą samą wartością	dopisujemy 0 po przecinku: 0,10
0,125	2^-1=0,125	0,125<=0,125, więc: a=0,125-0,125=0, czyli nasz algorytm kończy swoje działanie	dopisujemy 1 po przecinku: 0,101

#include<iostream>
using namespace std;
void to_binary(double x)
//deklarujemy funkcje z jedną zmienną, którą będziemy zamieniać na system binarny
{	
    double wynik=0, w=0.1, a=0.5;
    //deklarujemy zmienną na wynik, zmienną w, aby kolejne cyfry wstawiać w odpowiednie 
    //miejsce oraz zmienną a, której przypisujemy watość 2 do potęgi -1.
    while(x>0)
    //dopóki x jest większe od zera
    {
        if(x>=a)
        //jeżeli x jest większy bądź równy a, od x odejmujemy a oraz do wyniku 
        //dodajemy 1 pomnożone przez w aby dodać je w odpowiednie miejsce
        {
            x=x-a;
            wynik=wynik+1*w;
        }
        w=w/10;
        //zmienną w dzielimy przez 10
        a=a/2;
        //zmienną a dzielimy przez 2, aby uzyskać kolejną ujemną potęga 2. 
    }
    cout<<wynik;
    //wyświetlamy wynik
}
int main()
{
    double x;
    cin>>x;
    to_binary(x);
    //wywołujemy funkcję dla odpowiedniego argumentu
}

ZADANIE: Napisz program, zamieniający ułamek zapisany w systemie binarnym na ułamek zapisany w systemie dziesiętnym.