Sortowanie
Sortowanie bąbelkowe (bubble sort):
Algorytm sortowania bąbelkowego to najprostszy z algorytmów sortujących.
– prosty w implementacji
– nieoptymalny dla dużych zbiorów liczbowych
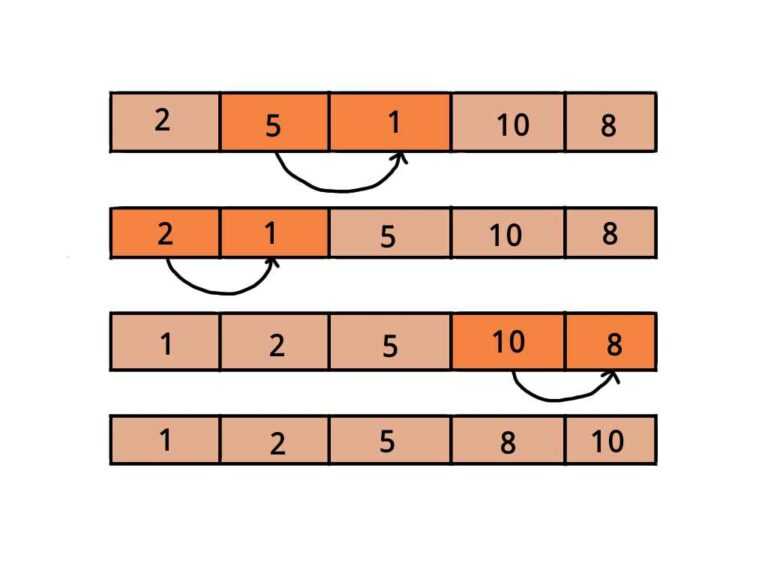
Działanie algorytmu sortowania bąbelkowego:
– bierzemy kolejno liczby z tablicy z danymi, zaczynamy od elementu o indeksie 0
– porównujemy go do kolejnego elementu – o indeksie 1, jeżeli jest on od niego większy, to zamieniamy liczby miejscami
– wykonujemy to działanie dla wszystkich elementów tablicy i na końcu otrzymujemy tablicę z posortowanymi danymi
Przykładowa implementacja:
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
int tab[n]; //deklarujemy tablicę o wczytanym wcześniej rozmiarze
for(int i=0;i<n;i++)
cin>>tab[i]; //wczytujemy danę do tablicy
for(int i=0;i<n;i++) //przechodzimy przez całą tablicę za pomocą funkcji for
{
for(int j=1;j<n-i;j++)
//następnie przechodzimy przez tablicę zaczynając od elementu o indeksie 1
//do elementu o indeksie n-i-1, czyli ostatniego elementu
//poprzedzającego tab[i]
{
if(tab[j-1]>tab[j])
//jeżeli poprzedni element jest większy, to zamieniamy je miejscami
//za pomocą funkcji swap()
{
swap(tab[j-1],tab[j]);
}
}
}
for(int i=0;i<n;i++)
cout<<tab[i]; //wypisujemy dane z posortowanej rosnąco tablicy
}
Złożoność:
Średnia złożoność czasowa algorytmu wynosi O(n^2), natomiast pamięciowa O(1).
ZADANIE: napisz program sortowania bąbelkowego, który uporządkuje dane malejąco.
Sortowanie przez wstawianie (insertion sort):
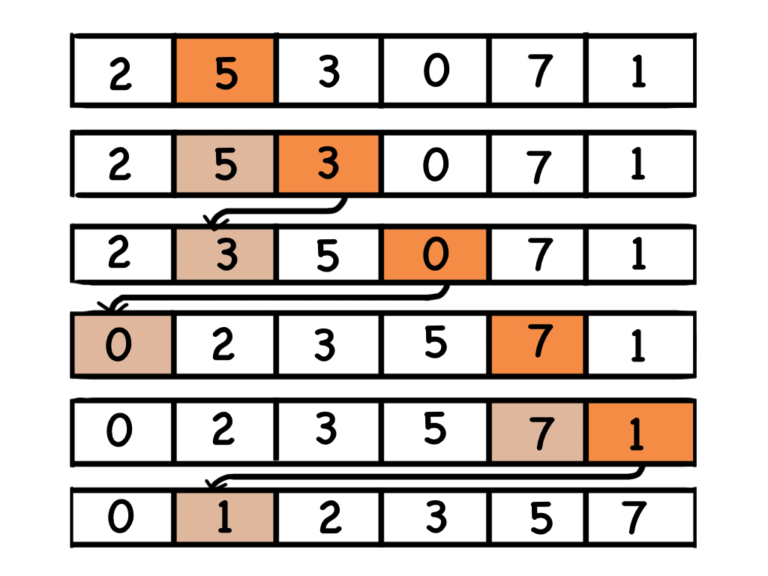
Jest to prosty algorytm, polegający na wstawianiu danego elementu na właściwą pozycję wśród uporządkowanych już elementów. Ciąg liczb jest dzielony na liczby posortowane i do posortowania. Algorytm kolejno porównuje elementy do posortowania z poprzednio uporządkowanymi, znajduje ich prawidłowe miejsce i wstawia je na nie.
-łatwy w implementacji
-wydajny dla niewielkich zbiorów liczb
Przykładowa implementacja:
#include <iostream>
using namespace std;
int main()
{
int n;
cin>>n; //długość naszego ciągu
int tab[n]; //ciąg który będziemy sortować rosnąco
for(int i=0;i<n;i++)
cin>>tab[i]; //wczytanie ciągu do tablicy
int j,pom;
for(int i=1;i<n;i++) //zaczynamy od 2 elementu i przechodzimy po całym ciągu
{
pom=tab[i]; //tworzymy zmienną pomocniczą
j=i-1; //ustawiamy j na poprzednią liczbę w ciągu
while(j>=0 && tab[j]>pom)
//znajdujemy w którym miejscu trzeba wstawić liczbę,
//przechodząc po ciągu dopóki się nie skończy i dopóki nasza liczba
//jest mniejsza od poprzedniej
{
tab[j+1]=tab[j]; //przesuwamy dotychczasowe elementy
j--;
}
tab[j+1]=pom; //wstawiamy nasz element na jego miejsce
}
for(int i=0;i<n;i++)
cout<<tab[i]<<" "; //wypisujemy wynik końcowy - posortowaną tablicę
}
Złożoność:
Średnia złożoność czasowa naszego algorytmu wynosi O(n^2), natomiast pamięciowa wynosi O(1).
ZADANIE: napisz program sortowania przez wstawianie, który uporządkuje dane malejąco
Sortowanie przez zliczanie (counting sort):
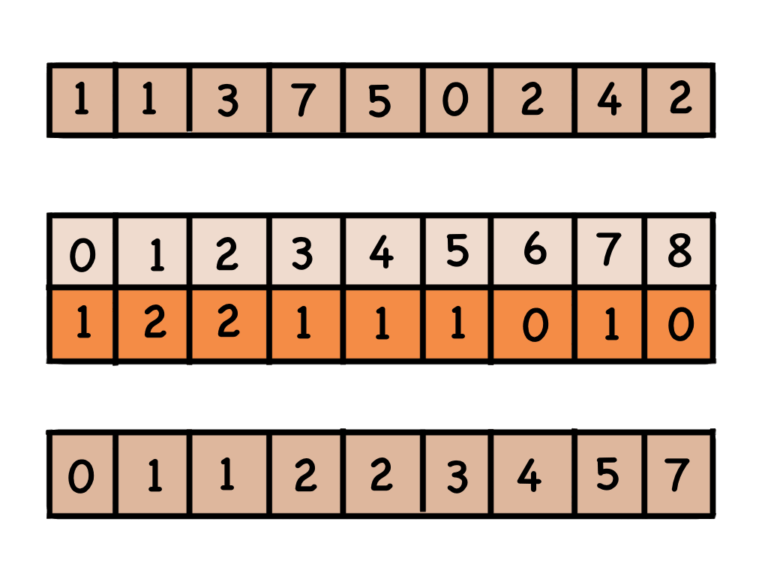
W przeciwieństwie do innych algorytmów sortowania zamiast porównywać dane między sobą polega na zliczaniu częstotliwości ich występowania i wypisywaniu ich kolejno odpowiednią ilość razy.
-łatwy w implementacji
-niewydajny dla dużych zbiorów
-zajmuje dodatkowe miejsce na zliczenie częstotliwości liczb
Przykładowa implementacja:
#include <iostream>
using namespace std;
int main()
{
int n; //długość naszego ciągu
cin>>n;
int tab[n]; //nasz ciąg
int licznik[n]={0};
//wypełniamy zerami tablicę w której będziemy zliczać częstotliwość wystąpień
for(int i=0;i<n;i++) //wczytujemy nasz ciąg
{
cin>>tab[i];
licznik[tab[i]]++;
//dla każdej liczby która wystąpi zwiększamy częstotliwość jej wystąpień
}
for(int i=0;i<=n;i++)
{
while(licznik[i]>0)
//wypisujemy kolejne liczby dopóki ich licznik jest większy od 0,
//czyli tyle razy ile wystąpiły w ciągu początkowym
{
cout<<i<<" ";
licznik[i]--; //pamiętajmy zmniejszyć licznik
}
}
}
Złożoność:
Średnia złożoność czasowa i pamięciowa wynosi O(n+m).
ZADANIE: napisz program sortowania przez zliczanie, który uporządkuje dane malejąco
Sortowanie szybkie (quick sort):
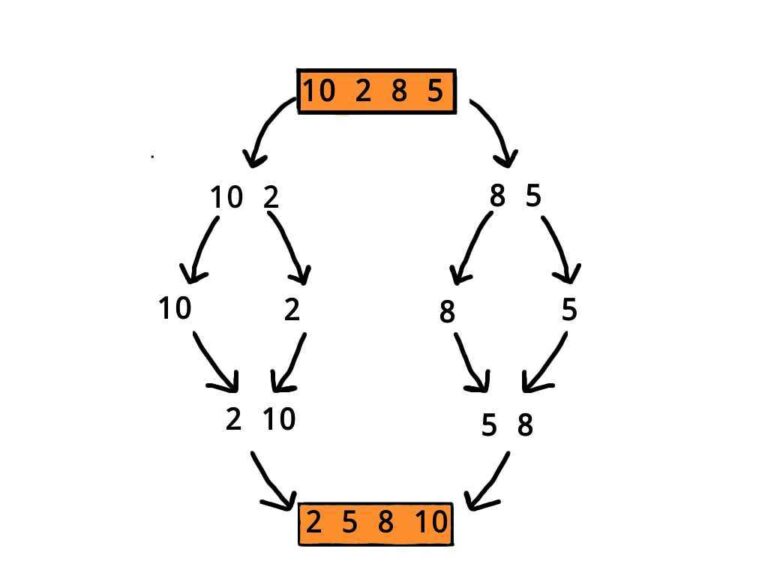
Quicksort to algorytm oparty na zasadzie “Dziel i zwyciężaj”. Dane dzielimy względem “pivota” czyli środkowego elementu, a następnie jeżeli po lewej stronie pivota znajdują się liczby od niego większe przerzucamy je na drugą stonę, analogicznie postępujemy z liczbami po prawej stronie. Jest to jeden z najszybszych algorytmów sortujących.
– jest łatwy w implementacji
– jest niestabilny, jego złożoność czasowa może być różna w zależności od danych
Przykładowa implementacja:
#include <iostream>
using namespace std;
// deklarujemy funkcję do sortowania fragmentu tablicy za pomocą algorytmu
//Quicksort argumenty: tab[]- nazwa tablicy, którą chcemy posortować,
//low - indeks pierwszego elementu tablicy
//high - indeks ostatniego elementu tablicy
void quicksort(int tab[], int low, int high)
{
if(low<high)
{
// Wybieramy element dzielący (pivot) - środkowy element
//sortowanego przedziału
int pivot=tab[(low+high) / 2];
int i = low;
int j = high;
// Podział na dwie części - od i do pivota i od j do pivota
while (i<=j)
{
// Znajdujemy element do zamiany z lewej strony
//czyli pierwszy element w rozważanym przedziale większy od pivota
while (tab[i] < pivot)
i++;
// Znajdujemy element do zamiany z prawej strony
// czyli pierwszy element w rozważanym przedziale mniejszy od pivota
while (tab[j] > pivot)
j--;
// Jeśli program znalazł takie elementy, to zamieniamy je
//i zmniejszamy przedział do kolejnego sortowania
if (i <= j)
{
swap(tab[i],tab[j]);
i++;
j--;
}
}
//Wywołujemy rekurencyjnie funkcję quicksort dla lewej i prawej części
quicksort(tab, low, j);
quicksort(tab, i, high);
}
}
int main()
{
int n;
cin>>n;
int tab[n];
for(int i=0;i<n;i++)
cin>>tab[i]; //wczytujemy dane
quicksort(tab,0,n-1); //wywołujemy funkcję quicksort dla odpowiednich argumentów
for(int i=0;i<n;i++)
cout<<tab[i]<<" ";
//wyświetlamy wszystkie elementy już posortowanej tablicy
}Złożoność:
Złożoność czasowa algorytmu wynosi od O(n logn) do O(n^2) – w sytuacji pesymistycznej. Złożoność pamięciowa wynosi O(1).
ZADANIE: Napisz program sortowania szybkiego, który uszereguje liczby malejąco.

Idealne miejsce aby zacząć swoją przygodę z programowaniem.
Copyright © 2024 return help;
