Największy Wspólny Dzielnik
NWD to skrót od “Najmniejszego wspólnego dzielnika” dwóch podanych liczb, czyli największej liczby naturalnej dzielącej obydwie podane liczby np:
NWD(18, 48) = 6 NWD(4, 17) = 1
Liczby względnie pierwsze, to takie liczby, których najmniejszym wspólnym dzielnikiem jest 1.
NWD wykorzystujemy do skracania ułamków bądź znajdowania ich NWW – “Najmniejszej wspólnej wielokrotności”, czyli najmniejszej liczby naturalnej będącej wielokrotnością obydwóch podanych liczb:
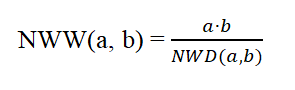
Algorytm Euklidesa:
NWD możemy obliczyć za pomocą algorytmu Euklidesa, który działa w następujący sposób:
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
while(a != b)
{
if(a > b)
{
a = a - b;
// dopóki liczby a i b nie są sobie równe to od większej z nich
//odejmujemy mniejszą
}
else
{
b = b - a;
}
}cout << a; // jest to wywołanie równoważne z "cout << b;", ponieważ pętla
} // while kończy swoje działanie, gdy liczby a i b są sobie równeDziałanie powyższego algorytmu dla a = 24 i b = 42:
a | b | Działanie | |
24 | 42 | b>a, więc: b=b-a=42-24=18 | 1 |
24 | 18 | a>b, więc a=a-b=24-18=6 | 2 |
6 | 18 | b>a, więc: b=b-a=18-6=12 | 3 |
6 | 12 | b>a, więc: b=b-a=12-6=6 | 4 |
6 | 6 | a=b=6, więc: NWD(a,b)=a=b=6 | 5 |
Działanie algorytmu dla a=73 i b=2, czyli liczb względnie pierwszych, takich że a jest ponad 36 razy większe niż b:
a | b | Działanie | |
73 | 2 | a=a-b=73-2=71 | 1 |
71 | 2 | a=a-b=71-2=69 | 2 |
69 | 2 | a=a-b=69-2=67 | 3 |
67 | 2 | a=a-b=67-2=65 | 4 |
Jak możemy zauważyć algorytm nie będzie działał optymalnie – aż 36 razy będziemy odejmować od liczby a liczbę b, aż uzyskamy:
1 | 2 | b=b-a=2-1=1 | 37 |
1 | 1 | NWD(a,b)=a=b=1 | 38 |
Jak możemy zauważyć nasz pierwszy algorytm będzie wykonywał bardzo dużo operacji dla np. liczb względnie pierwszych, z których jedna jest znacznie większa od drugiej. Dlatego możemy go zoptymalizować.
Zoptymalizowany algorytm Euklidesa:
Działanie zoptymalizowanego algorytmu Euklidesa:
#include<iostream>
using namespace std;
int main()
{
int a,b;
cin>>a>>b;
int pom; //deklarujemy zmienną pomocniczą
while(b != 0) //pętle wykonujemy dopóki b jest różne od zera
{
pom = b; //zmiennej pomocniczej przypisujemy wartość b
b = a % b; //zmiennej b przypisujemy wartość reszty z dzielenia a przez b
a = pom; //zmiennej a przypisujemy wartość zmiennej pomocniczej,
} //czyli wartość liczby b na początku działania pętli
cout<< a; //wypisujemy na ekranie wartość zmiennej a, czyli NWD(a,b)
} Możemy teraz zauważyć, jak znacznie lepiej będzie działał zoptymalizowany algorytm dla pary liczb a=73 i b=2:
a | b | Działanie | |
73 | 2 | pom=b=2 b=a%b=73%2=1 a=pom=2 | 1 |
2 | 1 | pom=b=1 b=a%2=2%1=0 a=pom=1 | 2 |
1 | 0 | b=0, więc pętla kończy swoje działanie: NWD(73,2)=a=1 | 3 |
Zoptymalizowany algorytm wykonał zaledwie trzy operacje w przeciwieństwie do algorytmu pierwszego, który potrzebował ich aż trzydzieści osiem.
ZADANIE: Napisz program, obliczający NWW dwóch wczytanych z klawiatury liczb.
ZADANIE: Korzystając z algorytmu Euklidesa napisz program, który oblicza NWD czterech wczytanych z klawiatury liczb.
Algorytm Steina:
NWD dwóch dowolnych liczb możemy również obliczyć za pomocą algorytmu Steina.
Działa on w następujący sposób:
- Jeśli b jest większe od a, to zamieniamy liczby miejscami
- NWD(0, 0) = 0
- NWD(a,0) = a oraz NWD(0,b) = b
- Jeśli a i b są liczbami parzystymi to: NWD=2*(a/2,b/2)
- Jeśli a i b są liczbami nieparzystymi to: NWD(a,b)=NWD(a,(a-b)/2)
- Algorytm kończy swoje działanie, gdy a=0 lub b=0
#include<iostream>
using namespace std;
//piszemy funkcje obliczającą NWD dwóch podanych liczb
int NWD(int a, int b)
{
if (a == 0) return b;
if (b == 0 || a == b) return a;
// Deklarujemy zmienną, która będzie wynikiem NWD
int wynik = 1;
// Dopóki obie liczby są różne od zera
while (a!=0&&b!=0)
{
// Jeśli b jest większe od a, zamień miejscami a i b
if (b > a) swap(a, b);
// Jeśli obie liczby są parzyste, podziel obie przez 2
if (a % 2 == 0 && b % 2 == 0)
{
wynik *= 2;
a /= 2;
b /= 2;
}
// Jeśli tylko a jest parzyste, podziel a przez 2
else if (a % 2 == 0)
{
a /= 2;
}
// Jeśli tylko b jest parzyste, podziel b przez 2
else if (b % 2 == 0)
{
b /= 2;
}
// Jeśli żadna z liczb nie jest parzysta, od a odejmij b, a następnie podziel przez 2
else
{
int pom = (a - b) / 2;
a = b;
b = pom;
}
}
// Wynik NWD to iloczyn współczynnika 2 i pozostałej niezerowej liczby
return wynik * a;
}
int main()
{
int a, b;
cin >> a >> b;
//wczytujemy liczby oraz wywołujemy funkcje, podając je jako argumenty
cout << NWD(a, b);
return 0;
}
Działanie algorytmu:
a | b | Działanie | NWD |
12 | 36 | b>a, czyli zamieniamy liczby miejscami, a i b są liczbami parzystymi: a=36:2=18 b=12:2=6 | NWD=2NWD(18,6) |
18 | 6 | a i b są liczbami parzystymi: a=18:2=9 b=6:2=3 | NWD=2*2NWD(9,3) |
9 | 3 | a i b są liczbami nieparzystymi: a=(a-b):2=6:2=3 | NWD=2*2NWD(3,3) |
3 | 3 | a i b są liczbami nieparzytsymi: a=b=3 b=(a-b):2=0 | NWD=2*2NWD(3,0) |
3 | 0 | b=0, czyli algorytm kończy swoje działanie | NWD=2*2*3=12 |

Idealne miejsce aby zacząć swoją przygodę z programowaniem.
Copyright © 2024 return help;
