Metody przybliżone
Metody przybliżone służą do wyznaczenia jak najdokładniejszej wartości miejsca zerowego funkcji w danym przedziale (rozwiązań równania nie liniowego).
1. Metoda bisekcji (połowienia):
wykorzystuje strategię „Dziel i zwyciężaj”.
– Jest łatwa w implementacji
– zawsze jest zbieżna, jednak dosyć wolna
– jeżeli jest to funkcja, która jedynie dotyka osi, a nie przez nią przechodzi, nie da się znaleźć miejsca zerowego
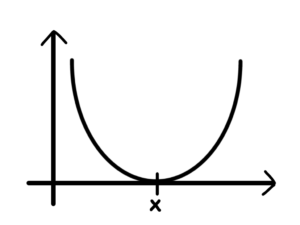
Aby nasz algorytm zadziałał pomiędzy dwoma punktami przedziału musi nastąpić zmiana znaku – jedna z przyjmowanych przez nie wartości jest ujemna a jedna dodatnia, co oznacza, że pomiędzy nimi znajduje się miejsce zerowe.
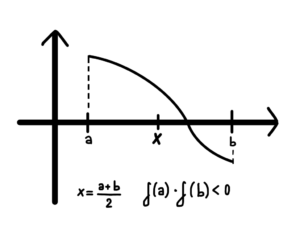
Polega na podziale naszego przedziału <a,b> w punkcie x=a+b/2. Jeżeli jest to wynik naszego równania zakańczamy nasz algorytm, a jeżeli nie to tworzymy nowe przedziały: <a,x> i <x,b> i sprawdzamy, który z tych przedziałów zachowuje nasz początkowy warunek zmiany znaku. Ponownie wykonujemy wszystkie kroki, dopóki różnica między punktami granicznymi naszego przedziału nie będzie mniejsza od przyjętego przez nas zaokrąglenia.
Przeanalizujmy algorytm na przykładzie funkcji x^2-2:
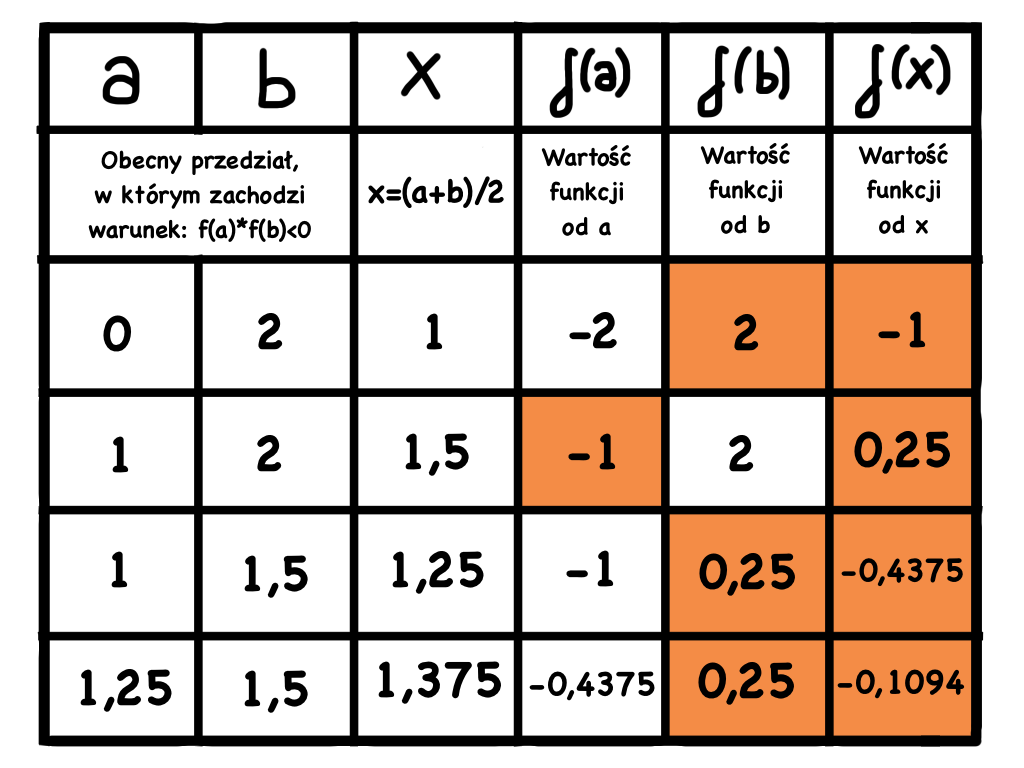
Przykładowa implementacja (dla funkcji x^2-2):
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{
int n=2;
//n to najwyższa potęga wielomianu, którego miejsce zerowe
//będziemy liczyć
double tab[n];
//tablica przechowuje kolejne współczynniki wielomianu
for(int i=0;i<=n;i++)
cin>>tab[i];
//wczytujemy -2, 0, 1 ponieważ takie od końca są
//współczynniki naszego wielomianu
double a,b;
cin>>a>>b;
//to przedział, w którym szukamy miejsca zerowego, czyli u nas 0-2
while(b-a>0.0001)
//program wykonuje się dopóki wielkość przedziału jest większa
//od założonego przez nas przybliżenia
{
double x=(a+b)/2; //tworzymy x, czyli środek przedziału
double wynik=0;
//wynik będzie przechowywał obecną wartość wielomianu dla x
for(int i=n;i>=0;i--)
//wykorzystując schemat hornera liczymy wartość wielomianu
{
wynik*=x;
wynik+=tab[i];
}
if(wynik>0)
//odpowiednio zmieniamy przedziały w zależności od uzyskanego
//wyniku
a=x;
if(wynik==0)
//jeżeli wynik jest równy 0 to znaleźliśmy miejsce zerowe
{
cout<<setprecision(5)<<fixed<<x<<"\n";
//funkcja setprecision wyświetli nasz wynik z dokładnością
//do podanej liczby miejsc po przecinku
return 0;
}
if(wynik<0)
b=x;
}
cout<<setprecision(5)<<fixed<<(a+b)/2<<"\n";
}
2. Metoda siecznych:
– jest dokładniejsza niż bisekcja
– jest szybsza od bisekcji
– aby metoda zadziałała funkcja nie może być stała
– może nie być zbieżna do pierwiastka
Korzystając z tej metody również używamy własności f(a)*f(b)<0. Wyprowadzamy wzór na sieczną, która połączy dwa punkty graniczne przedziału w punkcie x i sprawdzamy czy wyznaczony punkt jest naszym miejscem zerowym, jeżeli nie to tak jak w metodzie bisekcji zawężamy przedział.
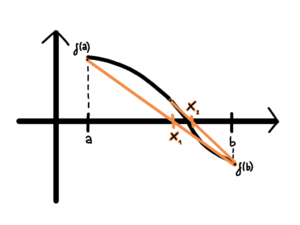
Wyznaczanie wzoru na miejsce zerowe:
wzór na równanie kierunkowe prostej:
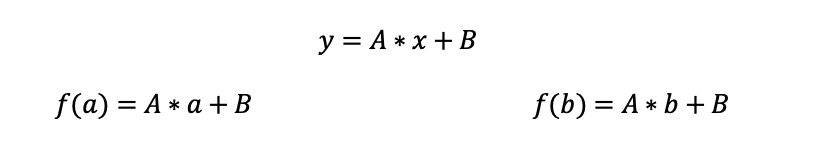
wyznaczamy współczynniki ze wzoru na równanie kierunkowe prostej, która przechodzi przez dwa punkty:
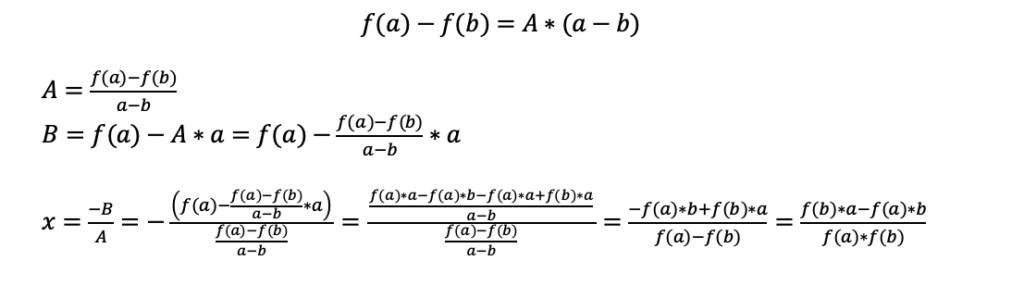
Przykładowa implementacja (dla funkcji x^2-2):
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int function(double x)
{
return x*x-2;
//tworzymy funkcję, która policzy wartość naszego wielomianu
}
int main()
{
double a,b,x,fa,fb,fx;
cin>>a>>b; //a i b to zakres naszego liczonego przedziału
fa=function(a);
fb=function(b); //liczymy wartości funkcji od a i b
while(b-a>0.0001)
//podobnie jak w bisekcji liczymy dopóki wielkość przedziału
//jest większa od wybranego przybliżenia
{
x=a-fa*(a-b)/(fa-fb);
//według wyprowadzonego wcześniej wzoru liczymy x
fx=function(x); //oraz wartości funkcji od x
if(fx>0) //tak samo jak w bisekcji zawężamy przedziały
a=x;
if(fx==0)
{
cout<<setprecision(5)<<fixed<<x<<"\n";
//oraz wypisujemy wynik w wybranym przybliżeniu
return 0;
}
if(fx<0)
b=x;
}
cout<<setprecision(5)<<fixed<<(a+b)/2<<"\n";
}

Idealne miejsce aby zacząć swoją przygodę z programowaniem.
Copyright © 2024 return help;
